LovesTheTeam.com

การเรียนการสอน

1

แบ่งการแสดงออกของรากย่อยออกเป็นปัจจัยง่ายๆ ดูปัจจัยใดที่ทำซ้ำหลาย ๆ ครั้งตามที่ระบุไว้ในตัวบ่งชี้ ราก, หรือมากกว่า ตัวอย่างเช่นคุณต้องแยกรากลูกบาศก์ออกจากจำนวนหนึ่งในกำลังที่สี่ ในกรณีนี้ตัวเลขสามารถแสดงเป็น * a * a = a * a * a * a = a * a3 ตัวชี้วัด ราก ในกรณีนี้จะสอดคล้องกับปัจจัย a3 เขาต้องถูกนำออกมาเพื่อเป็นเครื่องหมายของความรุนแรง

2

จำคุณสมบัติของราก ออกจากใต้ เครื่องหมาย รุนแรงคือการกระทำ,ตรงกันข้ามกับการยกกำลัง นั่นคือในกรณีนี้จำเป็นต้องแยกรากลูกบาศก์ออกจากส่วนของนิพจน์ที่ให้ผลการดำเนินการนี้ในกรณีนี้เป็น a3 3 aa a3 a3 aa

3

ตรวจสอบการคำนวณ นี้เป็นสิ่งสำคัญโดยเฉพาะอย่างยิ่งถ้าคุณกำลังทำงานกับตัวเลขมากกว่าตัวอักษรที่มีตัวแปรที่ทำเครื่องหมายไว้ ตัวอย่างเช่นคุณต้องแปลงแสดงออก3√120 ขยายการแสดงออกที่รุนแรงของช่วงเวลาที่คุณจะได้รับ3√120 = 3√ (60 * 2) = 3√ (30 * 2 * 2) = 3√ (15 * 2 * 2 * 2) = 3√ (3 * 5 * 2 * 2 * 2) จากใต้ ราก สามารถปัจจัย 2. เรามีนิพจน์ 23 ตรวจสอบผลลัพธ์ เมื่อต้องการทำเช่นนี้คุณต้องป้อน ปัจจัย ภายใต้ราก, เบื้องต้นเพิ่มขึ้นในระดับที่เหมาะสม 23 = 8. ด้วยเหตุนี้23√15 = 3√ (15 * 8) = 3√2020

4

เมื่อต้องการสลายตัวเลขที่มีตัวเลขจำนวนมากเป็นปัจจัยง่ายๆให้ใช้เครื่องคิดเลข เป็นประโยชน์ที่จะทำเช่นนี้เมื่อทำงานกับ รากซึ่งมีมากกว่าสองตัวเลข เมื่อทำงานกับตัวแปรที่กำหนดด้วยตัวอักษรนี้ไม่ได้มีความสำคัญเท่าที่ควรเนื่องจากการคำนวณที่แน่นอนไม่จำเป็น

5

ใช้เครื่องมือค้นหา นี่เป็นสิ่งที่จำเป็นเช่นหาตัวคูณจำนวนเต็มที่ใหญ่ที่สุดที่สามารถนำออกมาจากใต้ได้ เครื่องหมาย รุนแรง ใช้ระบบ Nigma ในเครื่องมือค้นหาให้ป้อนหมายเลขและสิ่งที่คุณต้องทำด้วย ตัวอย่างเช่นป้อนนิพจน์ "120 factorize" คุณจะได้รับการตอบสนอง 23 (3 * 5) นั่นคือเหมือนกับที่คุณได้จากการคำนวณด้วยวาจาในตัวอย่างที่กำหนด หากคุณต้องการคำนวณที่ถูกต้องให้ใช้เครื่องคิดเลขออนไลน์

คุณจะต้อง

• - ที่จับ;
• - กระดาษ;
• - ตารางรากลอการิทึม

การเรียนการสอน

1

เพื่อที่จะออกจาก เครื่องหมาย รากจินตนาการและเขียนนิพจน์ใต้อนุภาคเป็นผลิตภัณฑ์ของปัจจัยดังกล่าวเพื่อให้คุณสามารถแยกรากเลขคณิตจากที่หนึ่ง รากเลขที่ของการศึกษาระดับปริญญาจาก a คือจำนวน b เมื่อมันถูกยกขึ้นมาเป็นอำนาจโดยพลการนี้มันจะส่งผลให้จำนวน a. ในระหว่างการดำเนินการตามขั้นตอนนี้การแสดงออกของผู้ใต้บังคับบัญชาซึ่งประกอบไปด้วยปัจจัยต่างๆแล้วไม่ได้มาจากหมายเลขหนึ่งจะยังคงอยู่และเขียนขึ้นภายใต้เครื่องหมาย ราก.

2

ใช้ค่าเลขคณิตต่อไปนี้ ราก: เพื่อแยกเลขคณิต ราก จากการทำงานจำเป็นต้องแยกรากออกจากแต่ละปัจจัยแยกกัน เมื่อใช้คุณสมบัตินี้ในขั้นตอนนี้คุณจะได้รับแทนปัจจัยผลิตภัณฑ์ภายใต้เครื่องหมายเดียว ราก สองต่างกัน ราก มีสองนิพจน์รอง

3

แยกรากของนิพจน์ย่อยที่เป็นผลลัพธ์ออกต่างหากถ้าเป็นไปได้ การสกัด ราก คือการกระทำเกี่ยวกับพีชคณิตผกผันกับการยกกำลัง การสกัด ราก ขององศาโดยพลการจากจำนวนหมายถึงการหาจำนวนที่เมื่อยกอำนาจตามอำเภอใจนี้จะส่งผลให้จำนวนที่กำหนด ถ้าการสกัด ราก เพื่อให้เป็นไปไม่ได้ให้ปล่อยให้ความรู้สึกที่เร่าร้อนอยู่ใต้ป้าย ราก เหมือนเดิม อันเป็นผลมาจากการกระทำเหล่านี้คุณจะทำการถอดถอนจาก เครื่องหมาย ราก.

การเรียนการสอน

1

การใช้ตัวคูณร่วมกันสำหรับ วงเล็บ - หนึ่งในวิธีที่พบมากที่สุดแฟ เทคนิคนี้ใช้เพื่อลดความซับซ้อนของโครงสร้างการแสดงออกเกี่ยวกับพีชคณิตระยะยาวนั่นคือ ของพหุนาม ตัวคูณทั่วไปสามารถเป็นตัวเลขเป็นจำนวนเต็มหรือเป็นสองส่วนและสำหรับการค้นหาจะใช้คุณสมบัติการกระจายตัวของการคูณ

2

Number ดูอย่างใกล้ชิดที่สัมประสิทธิ์สำหรับแต่ละองค์ประกอบของพหุนามคุณสามารถแบ่งออกเป็นจำนวนเดียวกันได้ ยกตัวอย่างเช่นในนิพจน์ 12 •z³ + 16 •z² - 4 จะเห็นได้ชัด ปัจจัย 4. หลังจากแปลงแล้วเราจะได้ 4 (3 •z³ + 4 •z² - 1) กล่าวอีกนัยหนึ่งตัวเลขนี้เป็นตัวหารจำนวนเต็มที่น้อยที่สุดของค่าสัมประสิทธิ์ทั้งหมด

3

แบบเอกพจน์ตรวจสอบว่ามีตัวแปรเดียวกันในแต่ละเงื่อนไขของพหุนามหรือไม่ สมมติว่าตอนนี้ดูสัมประสิทธิ์แล้วเช่นในกรณีก่อนหน้านี้ ตัวอย่าง: 9 • z ^ 4 - 6 •z³ + 15 •z² - 3 • z

4

แต่ละองค์ประกอบของพหุนามนี้มีตัวแปร z นอกจากนี้ค่าสัมประสิทธิ์ทั้งหมดเป็นตัวเลขที่เป็นทวีคูณของ 3. ดังนั้นปัจจัยร่วมกันคือ monomial 3 • z: 3 • z • (3 •zφ - 2 •z² + 5 • z-1)

5

สมาชิกสองคน วงเล็บ กำหนดทั่วไป ปัจจัย ของสององค์ประกอบตัวแปรและจำนวนซึ่งเป็นทางออกของพหุนามทั่วไป ดังนั้นถ้า ปัจจัย-double เป็นเหตุผลแล้วคุณต้องพบอย่างน้อยหนึ่งราก เลือกระยะฟรีของพหุนามนี่คือค่าสัมประสิทธิ์โดยไม่มีตัวแปร ตอนนี้ใช้วิธีการทดแทนกับนิพจน์ทั่วไปของตัวหารทั้งหมดของจำนวนเต็ม

6

พิจารณาตัวอย่าง: z ^ 4 - 2 •z³ + z² - 4 • z + 4 ตรวจสอบว่าตัวหารจำนวนเต็มใด ๆ ของจำนวน 4 เป็นรากของสมการ z ^ 4 - 2 •zφ + z² - 4 • z + 4 = 0 ด้วยการหาสูตรง่ายๆให้หา z1 = 1 และ z2 = 2, วงเล็บ (z - 1) และ (z - 2) ในการค้นหานิพจน์ที่เหลือให้ใช้ส่วนต่อเนื่องในคอลัมน์

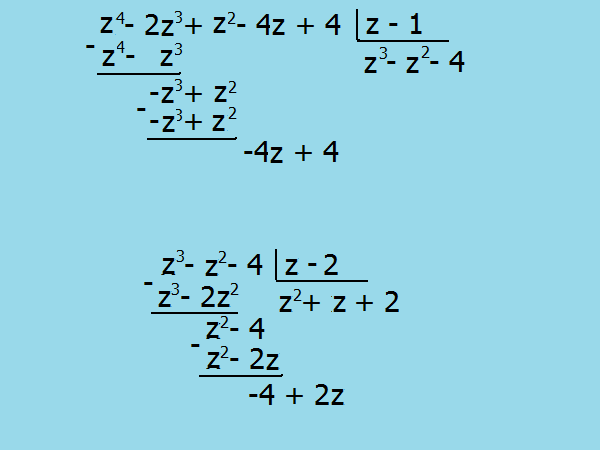
7

บันทึกผล (z - 1) • (z - 2) • (z² + z + 2)

การเรียนการสอน

1

พยายามที่จะขยายจำนวนเป็นปัจจัยสำคัญ หากตัวเลขเป็นเศษส่วนไม่นับจนถึงจุลภาคให้นับตัวเลขทั้งหมด ตัวอย่างเช่นจำนวน 8,91 สามารถขยายได้ดังนี้: 8,91 = 0,9 * 0,9 * 11 (ก่อนขยาย 891 = 9 * 9 * 11 จากนั้นเพิ่มเครื่องหมายจุลภาค) ตอนนี้คุณสามารถเขียนตัวเลขเป็น 0.9 ^ 2 * 11 และเอาออกจากรากของ 0.9 ดังนั้นคุณมี√8.91 = 0.9√11

2

ถ้าคุณได้รับรากลูกบาศก์คุณต้องที่จะอนุมานได้ในจำนวนที่สาม ตัวอย่างเช่นจำนวน 135 จะขยายเป็น 3 * 3 * 3 * 5 = 3 ^ 3 * 5 จากรากพิมพ์ตัวเลข 3 จำนวน 5 ยังคงอยู่ใต้เครื่องหมายราก ทำเช่นเดียวกันกับรากที่สี่และสูงกว่า

3

เพื่อให้ได้มาจากหมายเลขรากที่มีองศาแตกต่างจากระดับของราก (ตัวอย่างเช่นรากเป็นรูปสี่เหลี่ยมจัตุรัสและด้านล่างเป็นจำนวน 3 องศา) ให้ทำดังนี้ เขียนรากลงไปในระดับหนึ่งคือถอดเครื่องหมาย√ออกแล้วใส่เครื่องหมายปริญญาแทน ตัวอย่างเช่นรากที่สองของจำนวนเท่ากับจำนวนเดียวกันในอำนาจของ½และรากลูกบาศก์ให้อำนาจของ 1/3 อย่าลืมใส่นิพจน์ในวงเล็บ

4

ลดความซับซ้อนของการแสดงออกด้วยการคูณองศา ตัวอย่างเช่นถ้าใต้รากมีจำนวน 12 ^ 4 และรากเป็นรูปสี่เหลี่ยมผืนผ้าการแสดงออกจะมีรูปแบบ (12 ^ 4) ^ 1/2 = 12 ^ 4/2 = 12 ^ 2 = 144

5

มาจากด้านล่างเครื่องหมายรากและสามารถลบจำนวน ถ้าองศาเป็นเลขคี่เพียงแค่แทนจำนวนที่อยู่ใต้รากเป็นจำนวนเท่ากันตัวอย่างเช่น -8 = (-2) ^ 3 รากของก้อน (-8) จะเท่ากับ (-2)

6

เพื่อให้เป็นตัวเลขลบจากใต้รากแม้องศา (รวมถึงสี่เหลี่ยมจัตุรัส) ให้ทำเช่นนั้น ลองจินตนาการถึง radicand ในรูปของผลิตภัณฑ์ (-1) และตัวเลขตามระดับที่ต้องการแล้วนำตัวเลขออก (-1) ใต้เครื่องหมายราก ยกตัวอย่างเช่น√ (-144) = √ (-1) * √144 = 12 * √ (-1) ในกรณีนี้จำนวน√ (-1) ในวิชาคณิตศาสตร์มักเรียกว่าเป็นจำนวนเชิงซ้อนและแสดงด้วยพารามิเตอร์ i ดังนั้น√ (-144) = 12i